Ray Triangle Intersection

Step 1: Triangle::hit

The first intersect routine that the hit routines for the triangle mesh in student/tri_mesh.cpp.

We recommend that you implement the Moller-Trumbore algorithm, a fast algorithm that takes advantage of a barycentric coordinates parameterization of the intersection point, for ray-triangle intersection.

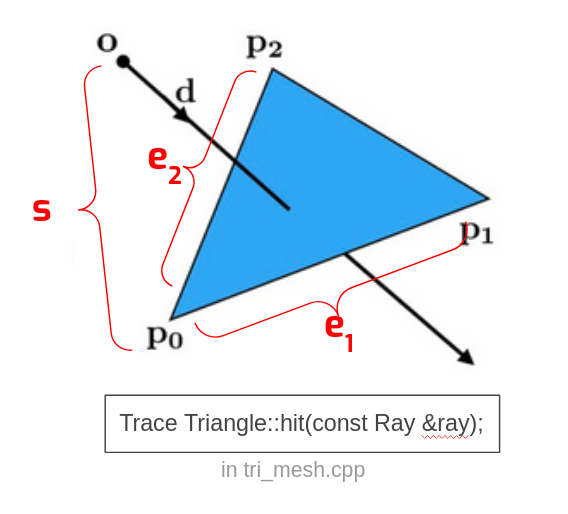
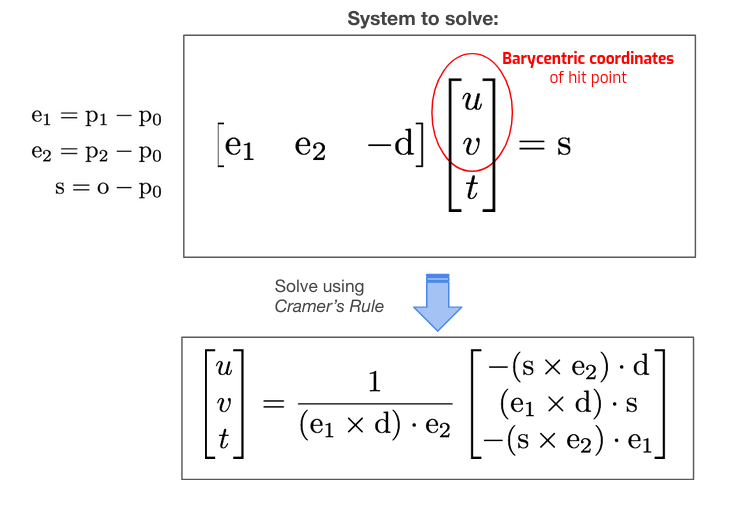
There are two important details you should be aware of about intersection:

• When finding the first-hit intersection with a triangle, you need to fill in the Trace structure with details of the hit. The structure should be initialized with:

  • hit: a boolean representing if there is a hit or not.
  • distance: the distance from the origin of the ray to the hit point.
  • position: the position of the hit point. This can be computed from ray.at(distance).
  • normal: the shading normal of the surface at the hit point. The shading normal for a triangle is computed by linear interpolation from per-vertex normals using the barycentric coordinates of the hit point as their weights. The shading normal for a sphere is the same as its geometric normal.
  • origin: the origin of the query ray (ignore).
  • material: the material ID of the hit object (ignore).

Once you’ve successfully implemented triangle intersection, you will be able to render many of the scenes in the media directory. However, your ray tracer will be very slow!

Tip: While you are working with student/tri_mesh.cpp, you can choose to implement Triangle::bbox as well (pretty straightforward to do), which is needed for task 3.

A few final notes and thoughts:

• If the denominator dot((e1 x d), e2) is zero, what does that mean about the relationship of the ray and the triangle? Can a triangle with this area be hit by a ray? Given u and v, how do you know if the ray hits the triangle? Don’t forget that the intersection point on the ray should be within the ray’s dist_bounds.
• Don’t use abs(). In GCC, this is the integer-only absolute value function. To get the float version, use std::abs() or fabsf().